BQ #7: Origin of the Difference Quotient

What is the difference quotient?
The difference quotient is the formula in order to deduce the slope of a line that touches a curve on the graph. It allows us to be able to find any slope of any line at any point. It essentially is very similar to the slope formula where the main formula is the change of y divided by the change of x. The main difference here is that the difference quotient, we label the change in y as f(x) while in the slope formula, we see that we instead use the change of y as the y-axis.

Slope Formula

In order to understand the difference quotient, we must explain how it relates to the slope formula. If we use what we learned earlier, we would change this equation to the change of y over the change of x. The issue with this equation is that it is only applicable to straight, non-curved lines. In order to find a curved one, we must use another formula, which is where the difference quotient comes into play.

Difference Quotient

Where this equation comes from is where a line passes through two main points at A and B, which is
 (x, f(x)) as well as (x+h, f(x+h)). This is essentially also called the secant line.
                                                             
                                                     http://www.analyzemath.com/calculus/Differentiation/difference_quotient.html
Furthermore the change of x is basically h. This is where we get delta x from. To not be mistaken, the difference quotient is not used only for curved lines. In fact, we can also use it for straight lines as well. It is therefore a paramount concept that will most definitely be a boon in calculus. To actually find the slope of a line given this formula, we use the difference quotient in order to find the derivative. We do not directly find the slope from the difference quotient. In fact, it is a multiple step process that involves us to find the derivative. After we do so, we input the value of x into the resulting derivative to get our slope. The tangent line is merely what the secant line is trying to get closer to as we solve for the derivative. We take the limit as a point and another one move closer to one another, which is how we find our tangent line. The difference quotient, all in all, is a method we use to find the slope of any line.

References:
http://www.analyzemath.com/calculus/Differentiation/difference_quotient.html
http://math.about.com/od/allaboutslope/ss/Find-Slope-With-Formula-JW.htm
http://www.tc3.edu/instruct/sbrown/calc/ln021.htm

BQ #6: Unit U: Concepts 1-8: Limits of Functions

What is continuity? What is discontinuity?

         Continuity is a term used to describe a function that you can draw without any breaks or stops, meaning your pencil does not lift from the paper. That means that there are no hole, no breaks, and no vertical asymptotes to halt the function. 

          Discontinuity is where there are those aforementioned terminologies which include point, jump, oscillating, and infinite discontinuities as well as oscillating behavior. These continuities fall under two categories: removable and non-removable discontinuities.

           Removable discontinuities consist of point discontinuities, which are also known as hole discontinuities. An open point is a characteristic of this discontinuity without any point above or below the y-coordinate. a function exists at this point on a function of a graph.

          

http://www.ck12.org/book/CK-12-PreCalculus-Concepts/r508/section/1.10/

        Non-removable discontinuities consist of:

-Jump Discontinuites which are characteristic of two points, 1 closed 1 open or two open, on top and bottom of one another and part of different functions. The reason why this is a discontinuity is because to construct the whole graph, one would need to life his or her pencil off the paper to continue drawing the graph. There is a jump in the graph.

http://www.sagemath.org/calctut/inflimits.html

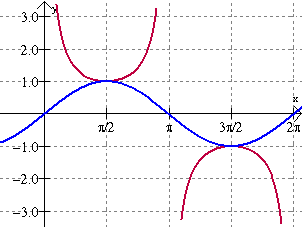
-Oscillating Behavior is when there is a wiggly function on the graph. There is little to explain other than this picture below.

http://www.sagemath.org/calctut/inflimits.html

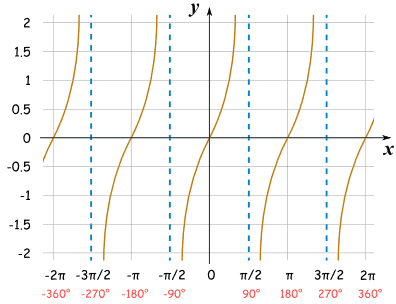
-Infinite Discontinuity is where there is a vertical asymptote that caused the graph to go to infinity and beyond...upwards and downwards. There is unbounded behavior when this occurs as the graph can reach indefinitely infinity where it increases or decreases without any bounds at all.

What is a limit?

A limit is basically the intended height of a function. We have a specific equation for this with lim f(x)=L with x->#. This equation is equivalent to saying the limit as x approaches a # of f(x) is equal to L. We never reach the limit because there are an infinite amount of values that we can write before we can actually reach the limit. An example would be reaching 2. From the left we would list values of 1.9, 1.99, 1.99, and etc., but we can never actually reach 2 because for all we know we can write 1.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999.

 By using a limit, we don't get the perfect answer. However, we want to fix and upgrade the values we want to make it close to being the perfect answer. The limit is very similar to what we want to find which is the instant change rate on the graph. 

How do we evaluate limits numerically, graphically, and algebraically?

             In order to evaluate limits numerically, a table must be drawn. There are 3 values of a number that should be listed to the left and right of the designated number, respectively. The ideal difference that should be shared between the middle # and the most left and most right numbers should be a tenth, 0.1.  The trick here is dealing with negative numbers. If we take -2, for example, the left number should not be -1.9, because that although that would be true for a positive 2, the left side must have a number that is lower than the designated value. -2.1 would therefore be the correct answer for the left of -2. Afterwards, you basically add a digit to the decimal place and get -2.01 in order to begin getting closer to the limit. The point here is that you do even though we do not get to the limit, we get closer and closer to it.
            To evaluate a limit graphically, we would draw the graph by inputting the function into the table.We would then place the point of our pencil on the graph at a position where the point is to the right of where x=a. We would then move the point along the graph to x=a from the right of the graph. Whatever value the y-coordinate approaches should be where our limit is. We do the same thing except from the left of x=a.
            Evaluating a limit algebraically we can use three methods:
-Direct substitution. Sometimes merely inputting the value of the limit can yield results we want. If we get a an answer that is not 0/0, which means indeterminate form, then we are done. However, when 0/0 is the case, we need to utilize other methods.
-Factoring. We can factor out the numerator and denominator the best we can and when we get a more simplified equation, we can then plug in the value of the limit to find our answer.
-Conjugating. We can multiply the top and bottom by the conjugate to find the limit. By multiplying the numerator and denominator, we are attempting to do the same thing as factoring. We are trying to cancel anything from the equation in order to further simplify it to then use substitution to get our answer.

http://www.ck12.org/book/CK-12-PreCalculus-Concepts/r508/section/1.10/

http://www.sagemath.org/calctut/inflimits.html

http://idiotsguides.com/static/quickguides/math/calculus-101-what-is-a-limit.html
http://people.hofstra.edu/stefan_waner/realworld/tutorials/frames2_6b.html
http://www.mathsisfun.com/calculus/limits-evaluating.html

BQ #4: Unit T- Concept 3

Why is a normal tangent graph uphill, but a normal cotangent graph downhill? Use unit circle ratios to explain.
Tangent: The reason why a normal tangent graph is uphill is because of its unit circle ratio of y/x. Because y/x is the equivalent to sin/cos, we see that whenever cos, or x, equals 0, there will be a vertical asymptote at that point. In this case, a tangent graph has asymptotes at π and 3π/2. Also, tangent is positive in quadrant 1 and 3 while being negative in 2 and 4. We can label the quadrants by every π mark starting at π/2, and label -π/2 as quadrant 4. Since we know in which quadrant tangent is positive, we draw the line ascending from the negative quadrant into the positive quadrant.

Cotangent: The cotangent graph is downhill due to its ratio of x/y. In this case, there is a vertical asymptote whenever sine equals 0. This occurs at π and 2π. The quadrants in which it is negative and positive is relatively the same as tangent. However, the location of the asymptotes starts at π and continues for every subsequent period of π. That means that we have an asymptote starting at the 0 mark and the π mark while it continues infinitely. We label every π/2 interval as a quadrant, and therefore we see that in quadrant 1 the graph descends downward to quadrant 2 where it is positive, constituting its downhill direction.

BQ #3- Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others? Emphasize asymptotes in your response.

Tangent?
The graphs of sine and cosine relate to tangent in contrasting and comparing ways. They all begin positive in the first quadrant. However, in sine and cosine, they are π/2 apart in the intervals that they cross the x-axis, and the distance they are apart when on the same graph. The tangent graph,however, at the π intervals, is undefined due to the prevalence of asymptotes when x=0 and due to that value along that asymptote possibly being infinitely positive or infinitely negative. We see the tangent graph that, instead of the line going horizontally infinitely, goes vertically infinite with a range of (-∞,∞).

                                   http://www.mathsisfun.com/algebra/trig-sin-cos-tan-graphs.html
Cotangent?
In the case of cotangent, its graph goes downhill. Therefore, in comparison with the graphs of sine and cosine, whose graphs start out positive, cotangent beings at a negative angle. This assumes that all graphs start at a value of a=0. Cotangent, being an inverse of tangent, of course will still have asymptotes. The asymptotes are still the same distance as they were for a cotangent graph, π. The difference with tangent is that cotangent has asymptotes where y=0, or where sin equals 0.

                            http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm
Secant?
To graph a secant graph, just do the same thing you do with the cosine graph. The difference here is that the secant graph has parabolas drawn at the mountains and valleys of the shifted parent graph. Also, secant graphs have asymptotes at π/2 with a period of π, meaning that they repeat their asymptotes every π distance. due to their asymptotes, the parabolas can not pass them and thus go continuously upward or downward, as described in the picture below. Unlike sine and cosine graphs, a secant graph, just like tangent, cotangent, etc. does not have an amplitude because the graph goes continuously downwards or upwards, as aforementioned.

                               http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm

Cosecant?
Cosecant graphs are just like sine graphs, but like secant, has vertical asymptotes and parabolas after we graph the parent graph and its shifts. We draw the parabolas at the mountains and valleys of the graph just like the secant graph. The difference between cosecant and secant is that in one period, a cosecant graph has two parabolas instead of secant which has 1 parabola going downwards and 2 half-parabolas going upwards. I say that they are half-parabolas because the asymptote within one period limits it. If we were to graph more asymptotes the parabola would of course be whole. The cosecant graph has asymptotes have asymptotes which occur at π every π unit, as shown in the below video.

http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm

References:

http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm

http://www.mathsisfun.com/algebra/trig-sin-cos-tan-graphs.html

BQ #5-Unit T Concepts 1-3

Why do sine and cosine not have asymptotes, but the other four trig functions do? Use unit circle to explain.
Sine and cosine do not have asymptotes due to their ratios on the unit circle. To have asymptotes, you must have an undefined value. Therefore, to obtain an undefined value, a denominator of 0 must be held because you can not divide a number by 0 and not have it be undefined. Sine's ratio is y/r, while cosine'sis x/r. r can not equal 0 because on the unit circle it always equals 1. Therefore, sine and cosine can not have asymptotes. Csc and sec can have asymptotes because their ratios are inverse of sine and cosine. Their rarios are r/y and r/x. In this case, x and y can equal zero, representative of the points (0,1) and (1,0), if y and x can equal zero, and they are the denominators of the ratio, then those values would be undefined, thus constituting the prevalence of asymptotes. It is the same thing with cotangent and tangent. Their respective ratios are x/y and y/x. Since y and x can equal zero on the unit circle and are the denominators of the ratios, then there is a possibility for them to have asymptotes when graphed. An asymptote is, for these trig fuctions, a vertical dashed line that can not be passed on the graph because the graph can not have a value that sits on an undefined line. As a result, we have the other four trig functions besides sine and cosine to have parabolas because the lines we draw must approach the asymptotes but not pass them, while in sine and cosine that is not the case.

BQ#2- Unit T Intro

How do the trig graphs relate to the Unit Circle?
The graphs connect with the Unit Circle as when the curves approach a certain value, they are representative of the quadrant the value is in. For example, when the curve is between 0π and π/2, the curve is positive for all graphs because in quadrant 1, all trig functions are positive. the curve's y-value would therefore be above 0. For sine, the curve becomes negative after it reaches π because at that point sine is negative and thus the graph begins to curve downward below the y-value of 0.

Period?- Why is the period for sine and cosine 2π, whereas the period for tangent and cotangent is π?
The period for sine and cosine is 2π because it takes the entire rotation of the unit circle to alternate between a positive and negative value. sine beings positive in two quadrants as positive, then the next two as negative until it returns to the first quadrant as a positive once again. For cosine, the unit circle begins positive, with it passing two quadrants that are negative, then returns to being positive in the fourth quadrant. Graphically, the line shifts downward when its shift value corresponds to the appropriate unit circle quadrant. Tan only needs 1 π as its period because its shift to a negative from a positive only takes two quadrants instead of four. Tan is positive in the first quadrant but negative in the second.

Amplitude?- How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?
Amplitude is present in sine and cos because there is a restriction for sine and cosine, who can't be used for values of less than -1 and greater than 1. Other trig functions can, however. The reason why sine and cosine are restricted is that the unit circle has values that would not make sense if the value was less than or greater than 1. For sine, y/h, you can not make the opposite side bigger than the hypotenuse because it defies the whole concept of right triangles. It is a common understanding that the hypotenuse is always the largest side. When it is not, as when the value of y is 1, then of course we have a quadrant angle as an answer because if y is 1, then x must be 0, which would mean that the ordered pair would be (0,1), or 90*. It is similar for cosine as if cosine is bigger than 1, then the value of x/h would be greater than 1, an impossibility. If x is 1, then y must be 0, which has an ordered pair of (0,1), which can be either 0* or 360*.

Reflection #1: Unit Q: Verifying Trig Identities

1. What does it mean to verify an identity?
            When we verify an identity, it means that we are trying to solve the equation in such a way that when we solve for the left side of the equation, it will, in the end, equal to the right side. Verification is necessary to prove an identity to be valid. When we first solve one of these identities, we want to ignore the right side. The right side is the answer we are trying to get. We use a multitude of techniques to change the left side of the equation as to get it to the right side. We can use reciprocals, we can change the identities to another one, or we can factor out trigonometric functions. We can also, in the process, cancel anything that can be canceled out. All of these strategies are to reduce the left equation as to match the right side- the verified answer. When both sides match, then we have verified our identity.

2. What tips and tricks have you found helpful?
            Tips I have found helpful is methods of solving an identity equation. If you are stuck on finding the next step in an identity, I like to see my options: can I use reciprocals? Can I use factorization? Can something be canceled out? Did I properly changed my identities? Did I try to convert everything to sin and cos? I like to use these rules to guide my problem-solving . All in all, I like to use try to have at most two trig functions when I am solving and will try to get it that way through identities. A strong tip I have is to know your identities inside-out. It is apparent that you should know your identities to solve identities. Even though you may be able to use your SSS packet to see the identities, it is much better to know them from the top of your head in order to conserve time and because if you know the identities from your memory, you will be able to think of many different paths to solve an identity, thus becoming an expert at identities.

3. Explain your thought process and steps in verifying a trig identity, in general terms.
           I believe this question has been answered as I have explained it in my tips and in my answer in what it means to verify an identity. To clarify, I like to have many options at hand in solving trig identities. If the trig identity is straightforward, then of course I will take the quickest path to solving. However, when the identity consists of fractions and tan, cot, sec, etc., I prefer to conjure ways to solve them in the most simple way, through a variety of methods, as mentioned before. I find it best when I convert the original trig function to sin and cos. I then look for any times I can multiply the numerator by the reciprocal of the denominator so I can look to square trig functions. I find it more preferable to look for ways to square them because then I open the range of identities at my disposal. If that is not possible, I see if I can solve the equation by factorization. This is best done in fraction equations, as things usually cancel out. Overall, depending on the type of trig identity I have to solve, I like to use the corresponding, most efficient method to solve it. I just find factorization and reciprocal multiplication to be the two techniques I have used the most during the problems in this unit. So basically, I look at the type of problem I am doing, and I use the appropriate process, such as factorization, reciprocals, and changing identities.

SP#7: Unit Q Concept 2: Finding All Trig Functions Given One Trig Function+Quadrant

Please see our SP #7, made in collaboration with Nga Mai, by visiting her blog here. Also be sure to check out the other awesomely awesome posts on her blog.

I/D 3 Unit Q- Pythagorean Identities

1. sin^2x and cos^2x=1 comes from the Pythagorean theorem of x^2+y^2=r^2. We know that x/r equals cosine and y/r equals sine from the unit circle ratios as we should know that our trigonometric functions of cosine is adjacent over hypotenuse and sine is opposite over hypotenuse. Since in the unit circle we considered a side opposite of an angle to be opposite of the angle that is protruding from (0,0) in all cases, we can deduce that the adjacent value equals x and that the opposite value equals y. If we take the Pythagorean theorem and solved to make r^2 1 by dividing the whole formula by r^2, we get what we wanted which is (x/r)^2+(y/r)^2=1. As we already went over, x/r is cosine and y/r is sine, and since the equation is already squared, that is where we get our equation of sin^2x and cos^2x=1. The x value that accompanies the formula can be substituted for theta if we never knew it.

2. In order to derive the identity with Secant and Tangent, we start off with our standard formula of sin^2x+cos^2x=1. We want to get secant, so we divide the whole equation by cos^2x in order to get that one the right side. Once we have 1/cos^2x on the right side, we see that same ratio is secant itself, just used twice, so we substitute 1/cos^2x for secx. On the left side of the equation, we also see sin/cos being the identity for tan, so we substitute tan^2x for that since sin/cos was squared as well. Cos^2x/cos^2x is 1 because they are the same number, just one over the other. We then obtain our final formula of tan^2x+1=sec^2x.

3. Just like the last problem, we start off with our formula of sin^2x and cos^2x=1. We want to get cosecane and cotangent this time, so we divide the equation by sin^2x this time. We get sin^2x/sin^2x+cos^2x/sin^2=1/sin^2x. For the right side, we can substitute that for csc^2x because we know that one of our trig identities is that csc equals 1 over sin. We can sub sin^2x/sin^2x for 1 since they equal each other. We substitute cos^2x/sin^2x for cotangent because the identity of cotangent is cos/sin, or x/y. After we substitute everything, we get 1+cot^2x=csc^2x as our final equation.

Inquiry Activity Reflection

1. THE CONNECTION I SEE BETWEEN UNITS N, O,P, AND Q SO FAR is that they all utilize the unit circle as well as the Pythagorean theorem to solve a multitude of problems. 

2. IF I HAD TO DESCRIBE TRIGONOMETRY IN THREE WORDS, THEY WOULD BE sine, cosine, and tangent.

WPP #13&14 Unit P Concepts 6&7

This WPP was made in collaboration with a handsome fellow named Mason Nguyen. Please visit the other awesome posts on his blog at Masonnperiod1.blogspot.com.
1. Law of Sines
       Hannah and her friend Miley are going on a trip to Los Angeles. However, they are at different locations, being 100 miles apart. Hannah flies there in a helicopter at a degree of N 29* E. Miley drives there in a BMW at a degree of N 40* W. They finally arrive at Los Angeles and give each other patty cakes. What was the distance it took for Miley to get to Los Angeles?

 In the above picture, we see the set-up for the problem. Hannah and Miley are 100 miles from each other so thus that is our side value. We draw the north-south line to show our N 29* E angle and our N 40* W angle. x stands for the value which we want to find, which is the distance from Miley's starting point to L.A.

 We find our angles by subtracting the corresponding values we gotten from 90*. We get 61* and 50*. Since we know two values of our angles, we can easily solve for the third by subtracting the two angles from 180*. Therefore, 180-61-50=69. 69* is our third angle. Now that we have a "bridge," we can use the law of sines.

We set up the ratios as shown above. We then cross multiply to eliminate the fractions. We then try to get x alone by dividing by sin69. We plug in the right side to our calculator and thus get 93.68 as our answer.

2. Law of Cosines
        Hannah has appointments in two different places. She can't be in two places at once, or CAN SHE? She asks Justin Timberlake if she can borrow his cloning machine. She then clones herself and orders her Hannah duplicate to go due east to Bakersfield. Hannah herself goes northeast to Riverside. The angle they create is 046*. The Hannah clone travels 25 miles to Bakersfield. Hannah travels 50 miles to Riverside. How far are the two apart now?

 We label everything accordingly. Since the problem said for the clone to go due easy, we know that Bakersfield is directly east of the starting line. The clone traveled 25 miles while Hannah traveled 50, so we label those. We also label the angle as 46*. Now that we have SAS, we can use the law of cosines.

We plug in our numbers into the formula as so. Let us substitute the variable a for x so that we can use b and c for the other sides. The formula is thus, to put it variably, a^2=b^2+c^2-2(b)(c)cosA. We then get our value when we plug it all into the calculator (do it all in one step) and get our next value. We have to square the value due to a being squared, so then we get our answer of 37.26 (miles).

BQ #1- Unit P: Law of Cosines and Area of an Oblique Triangle

3. Law of Cosines- We need Law of Cosines because it can solve for any angle and side of any triangle. As long as we have the right information (three sides or a side angle side), we can easily solve for any value as it is derived from the distance formula. Since we know that on a triangle, angle C is at (b,0) and angle B is at (cCosA, cSinA) since b is the distance from angle B to between angle A and angle C (Since you draw a perpendicular line down angle B) we can derive the (b,0). Also, since c is the distance from angle C to between angle A and angle B, we can also derive the latter point.

                      https://www.youtube.com/watch?v=lPP-pABvwdA

In the above video, we see the method to deriving the Law of Cosines. We see our desired formula of a^2=b^2+c^2-2bccosA. However, how do we derive that formula? First of all, we draw a triangle (as shown in the video, not a right triangle) and label the corners appropriately as A,B, and C. We then label their opposing sides as a,b, and c. We then draw a perpendicular line down angle C as demonstrated in the video to form two right triangles. We now have to cut the c side into two different values. Label the left triangle as "x", and since that is x, then the other side's value must be c-x because c is the total side value while x is one portion of it. Now that we know all the side values (as variables) we can use the Pythagorean Theorem. For the left triangle, we have x^2+h^2=b^2 (remember that h is the height we made from cutting the triangle in 2). For the right triangle we have (c-x)^2+h^2=a^. We have to foil this, so after we do that, we get c^2-2cx+x^2+h^2=a^2
            Where do we go from this?  Since x^2+h^2 is present in both the left and right triangles, and since the left triangle says that it equals b^2, then we can substitute that in for the right triangle formula to make c^2-2cx+b^2=a^2. We can move b^2 to the front and have b^2+c^2-2cx=a^2. As we reverse the equation to make it more like our original, desired formula, we have a^2=b^2+c^2-2cx. The x value in that formula does not correspond to what we want, so how do we get it? We get it by using our first triangle and taking the cos of angle A to get cosA=x/b. We solve for x and get x=bcosA. We substitute that in for our formula and get the desired formula, thus deriving the Law of Cosines.

4. Area of an Oblique Triangle- As we already know in an ABC labeled triangle, the sin of angle C is h/a because like the last problem, we draw a perpendicular line down the middle angle to make 2 right triangles. Since sinC=h/a, then that also means that h=asinC when we solve for h. Now when we substitute our common area equation for h, we get A=1/2b(asinC), since t'he regular area equation is A=1/2bh. This relates to the area equation because we use both base and height as it does except that we go a step beyond by using our laws of sin to derive our formula.


       https://www.youtube.com/watch?v=gMnBMJwpyc0

In the above video, we see how an oblique triangle is derived. This formula is very simple. It is A=1/2bcsinA. Of course, there are variations, so it can also be 1/2acsinB or 1/2 absinC. When you know the SAS value of the triangle, then you can easily plug in the corresponding values and then plug into your calculator the equation. For example, in the video, you merely plug in 1/2 x 12 x 8 x sin(135) to get your answer.

References:
http://www.mathsisfun.com/algebra/trig-cosine-law.html
https://www.youtube.com/watch?v=gMnBMJwpyc0
https://www.youtube.com/watch?v=lPP-pABvwdA

WPP #12 Unit O Concept 10: Elevation and Depression

         1.)  Hannah realizes that she wants to glide down a building into a soft bush. She climbs a 500 ft building, reaches the top, and gazes down at the bush at an angle of 25 degrees 10'. If Hannah was to glide perfectly horizontally, then suddenly fall onto the bush, what would be the distance she traveled horizontally.

THE PROBLEM

In order to solve this problem, first we need to calculate the value of 25 degrees 10'. We accomplish this by placing 10 over 60 (because there are 60 seconds in a minute) to get 10/60 which simplifies to 1/6 which, in decimal form, is .17. After we get the angle value, we can utilize trig functions. In the below picture, I use tan.  Tan is y/x so we use 500/x. We don't want variables as the denominator so we multiply both sides by x. We have to get x by itself so we divide both sides by tan 25.17. Our answer is 1063.99 which rounds to 1064 ft.

                                                                       The Solution

          2.) Hannah, after landing on the bush, has just discovered that she is terrified of falling. She deduces that what she loves is parkour. She loves to jump from buildings to buildings. She climbs the same building as the last problem, but wants to jump to the top of a 1000 ft building. She looks at the top of that building at an angle of 32 degrees 6' and reassures herself that she is the queen of pop. There is no way that she can fail this measly task of jumping 500 feet. How far is the building she is currently on from the building she wants to jump to?

THE PROBLEM

 To solve this problem, we must again find the angle value. We take 6 and divide it by 60 to get 1/10 which is essentially .1 which we add to 32 of course. To find our opposite side, just take the side value of the big building and subtract it by the height of the smaller building. Once we have found that out, we can use a trig function. I am a fan of tan, so I used tan once again. It is the same old song and dance as we multiply both sides by x and then divide by tan 32.1 to get our answer of 797.068 which is simplified to 797.07 feet.

THE SOLUTION

I/D #2 Unit O: Deriving Patterns For Special Right Triangles

                                    Inquiry Activity Summary:
1. 30-60-90

Step 1.) I drew the equilateral triangle and labeled all sides 1 as well as labeling the degrees as 1. Because it is an equilateral triangle, all sides are equal. If all sides are equal as each other, then it makes sense that the angles are equal to each other as well. The angles also add up to 180 degrees as well, a golden rule for triangles.

 Step 2.) I splitted the triangle in two by drawing a line down the middle, creating two 30-60-90 triangles. By drawing a line down the middle, I separate the 1 value on the bottom into two 1/2 values. Also, the 60 degrees at the top becomes two 30 degree angles.

 Step 3.) In order to simplify things and make it a little easier, we will be using one of the triangles for this portion of the derivation.The only thing we are adding here is "b" to the opposing side of angle 60.

 Step 4.) We are going to be using good ol' classic Pythagorean Theorem to solve for "b." In step 1, we use the formula of a^2+b^2=c^2. In step 2, we plug in the values. In step 3, we square the values to get the resulting answers. We then, in step 4, subtract 1/4 to both sides to get b^2 by itself. We get an answer of b^2=3/4, but we don't want the exponent. We then square root both sides in step 5. In step 6, we get our answer as depicted below.

 Step 4.) We label the "b" value we solved for on the triangle. However, we have two fractions for the triangle. We want no fractions and thus we multiply every side by two to cancel out the fractions. We then receive a hypotenuse of 2.

 Step 5.) Why do we use "n"? Well, we need "n" in order to solve problems."n" allows us to find values of all sides of a 30-60-90 triangle since if we have one value of a side of a 30-60-90 triangle, we basically have all the side values. It is all a matter of solving for the other 2 hidden values. Of course, in this example we do not need to use "n" to find the other sides because they were already given. However, it is crucial to understand that without "n," it would be more difficult to identify all sides. Knowing just the "n" value is enough to completely solve a special right triangle. The sides of a 30-60-90 triangle regarding n are n, n radical 3, and 2n.

2. 45-45-90                                                                                                                                             

Step 1.) I drew a beautiful square as shown below. The sides are labeled 1 and right angles shown.                                                                                                                                            

 Step 2.) I diagonally splitted the square to turn it in two 45-45-90 triangles. The angles are cut into two 45 degree angles and now we can derive the pattern.

 Step 3.) Let us solve for one of the triangles. Ignore the radical 2=c. We are going to find "c" so we can find all sides of the triangle and consequently find the same value of "c" for the other triangle.

 Step 4.) Since we know 2 of the values of the sides, we are going to be using the theorem of Pythagorean. We input the values into their proper variables, with both 1 values going into a and b, respectively. We then square the 1's to get a value of....ONE! We then add the 1's together to get 2 and square it to get radical 2. That will be our value for c.

 Step 5.)We then place our glorious value of radical 2 smack daddy in the middle and we have just found the hypotenuse for TWO triangles! It's just like hitting two stones with one bird.

 Step 6.) But wait, we need to put the n's in our special right triangle as well to, as said before, indicate to create a sort of formula to solve any special right triangle problems. By using n, we can easily solve for the hypotenuse or for a side. The hypotenuse is n radical 2 and the side values for n are n and n. We just hav eto multiply n by radical 2 to get n radical 2 and divide n by radical 2 to get n.

Inquiry Activity Reflection:

1. Something I never noticed before about special right triangles is that they are very easy to solve once you break up the steps to solve them one by one.

2. Being able to derive these triangles myself aids in my learning because now I can apply these lessons to my special right triangles as I now know the pattern for solving both 30-60-90 triangles and 45-45-90 triangles.

I/D#1: Unit N: Concept 7: Unit Circle and Special Right Triangles.

Inquiry Activity Summary:
      In this activity regarding unit circles, we labeled 3 special right triangles according to the Special Right Triangle Rule which will tie in to our derivation of the unit circle.

1. In this picture, we see a 30 degree triangle. To go by this problem step, our numbers in circles are chronological, which means they are in order of what to solve for first. For number 1, we label the triangles according to the aforementioned rule, so our hypotenuse value is 2x, our x value is x radical 3, and our y value is x. We got these values by looking them up on google and applying them here in this problem. For step number 2, we first follow instructions by setting the hypotenuse's value to 1, then divide the value of every other side by the value of the hypotenuse, which is in this case, 2x. Therefore, the y value becomes 1/2, and the x value becomes radical 3/2. We now see the relations of the unit circle to this activity as the values of the sides are identical to the ordered pairs in the unit circle. Step 3,4, and 5 has us simply labeling the r,x, and y value, which are respectively shown in the picture. Step 6 has us draw the coordinate grid of this triangle, and this is where we see how this triangle is literally identical to what it is on the unit circle.

In this picture, the 45 degree triangle is represented. We will go step by step just like the last picture. For step 1, the labeling of this triangle is thanks to the internet, and the hypotenuse value is x radical 2 with the x and y values being x. How this is so is because the 45 degree triangle has two sides which are equal due to this triangle being an angle that is in the middle of 90 degrees. Step 2 has us again set the hypotenuse to 1. We then divide the x and y values by the hypotenuse value, which is x radical 2. We therefore get radical 2/2 for the x and y value because they are the same values. Steps 3,4, 5 are shown as the labeling of the sides and step 6 has the graph of this triangle, and as we can see, the angle is representative of the unit circle.

In this picture, we have a 60 degree triangle, which is basically the same as the 30 degree triangle but the x values and the y values are reversed. The labeling is the same, so step 1 remains unchanged, except that the labeling for x and y are of course different from the first picture in that they are now respectives of each other now. Step 2 has the hypotenuse as 2x, the x value as  1/2, and the y value as radical 3 over 2. We derived these numbers from the work shown in the picture. The steps 3,4, and 5 are shown above clearly. Step 6 is where we draw the triangle. In this example, the x and y swap off in order to get that 60 degree shape. 

4. This activity assisted me in deriving the unit circle by teaching me 3 of the most important degrees I need to know for this unit. The x and y values are identical to those on the unit circle and by recognizing these special right triangles I can label the unit circle accordingly and solve real problems with ease.

5. The quadrant the triangles in this activity lies on is the 1st quadrant. If I placed the triangles in quadrant two, then the x value will be negative. If I placed them in quadrant 3, then both values would be negative. If I placed them in quadrant 4, then the y value would be negative. In this picture we see the 3 triangles being placed in different quadrants. The 30 degree triangle has its x value as a negative just like we mentioned. The 45 degree triangle has both ordered pair values being negative. The 60 degree triangle has only its y value being negative.Another change that occurred was how the overall angle measurements of each angle has changed. the 30 degree triangle is a reference angle for sure, but is 150 degrees from the initial axis. The 45 degree triangle is 225 degrees, and the 60 degree triangle is 300 degrees.

Inquiry Activity Reflection:

1. The coolest thing I learned from this activity was how this related to the unit circle I did last year and how easier this activity made my life easier by teaching me the core basics of the unit circle. 

2. This activity will help me in this unit because I will be able to derive the unit circle with greater ease by knowing the most important degree properties: 30, 45, and 60. 

3. Something I never realized before about special right triangles and the unit circle is how easy it can be after you do this activity of how to solve the properties of the 30, 45, and 60 degree triangles.

RWA #1: Unit M Concept 4-6: Conic Sections In Real Life Scenarios

1. Parabola: the set of all points the same distance from a point, known as the focus, and a line, known as the directrix.
2. Regarding the standard form of a parabola, if the parabola has a vertical axis of symmetry, then the equation is 
(x-h)²=4p(y-k), with (h,k+p) being the ordered pair for the focus. A parabola with a horizontal axis of symmetry will have the standard equation of (y-k)^2=4p(x-h) and the focus ordered pair being (h+p,k). The difference between the two is whether x or y is in the front of the equation and where the p value goes in the ordered pair of the focus. Visually (graphically), a parabola looks like a curved line, with both arrows pointing in the same direction, but meeting in the middle along the aforementioned curved lines. What determines the direction of the parabola are two factors. If the value of p is positive, just like the graph, the parabola is bound to be going up or right.If p is negative, then of course, the parabola will go down or left.The second factor on determining the direction of the parabola is if the equation has an (x-h)^2 or (y-k)^2 as its standard form. If it is x^2, then the  graph goes up or down. If its y^2. then its left or right. The size of the parabola depends on the value of |a|. The smaller the value of |a|,then the wider the graph. A parabola with a |a| of 0.3 will be much wider than one with an |a| of 1. This applies if the standard form is expressed as y=ax^2+bx+c. In this case we place a heavier emphasis on p.
        An axis of symmetry shows the exact middle of a parabola where it touches the vertex. The vertex is the origin of the parabola, and its value depends on the h and k values of the standard form. Regarding its origin graphically, it is in between the focus and the directrix. The focus's value,as mentioned before, depends on if the graph's axis of symmetry is horizontal or vertical. If its vertical, then the ordered pair is (h,k+p).If its horizontal, (h+p.k) will be the ordered pair. The focus is situated WITHIN the parabola. What this means is that the focus will always be in the same direction as where the arrows of the parabolas point to. The directrix's value is the p value added or subtracted conversely to what it was added or subtracted for the focus. However, we do not write it as an ordered pair. We write it either equal to x or y, depending on if the value goes up or down, or in other words, on the the direction of the axis of symmetry. The value of p,as mentioned previously, takes the value of the coefficient of the non-squared coefficient of the variable and sets it to 4p. This value determines how far the focus and directrix will be from the vertex. A key note is that the directrix is always behind the parabola, or vertex, and the focus is always in front of the parabola,or vertex. The focus affects the shape of the parabola tremendously due to its connection with the eccentricity of the parabola. The closer the focus is to the parabola, the skinnier the parabola will be due to its relation with the difference between the focus and vertex being closer to 0. The closer a conic section is to 0, then the more circular it will be. Therefore, if the focus is farther away from the vertex, than the curves of the parabola will stretch and become less circular.
                               
                                https://people.richland.edu/james/lecture/m116/conics/conics.html

      This picture depicts the various parts of the parabola. The vertex is now clearly shown as the origin of the parabola, since that is where all the other factors revolve around. The directrix is shown below the parabola, as the parabola protrudes upwards. The focus is between the two curves, and the axis of symmetry shows the middle of the parabola. The d1 and d2 lines showcase that the distance from the focus to a point on the parabola to the directrix is the same for both lines. Also, in this graph, we see that the focus is considerably farther away from the vertex than common examples with a p value such as 1/16, so the graph becomes wider.

                           
                         http://xahlee.info/SpecialPlaneCurves_dir/Parabola_dir/parabola.html

3.      A real life example of a parabola would be a car's headlights. In this example, to describe why it is a parabolic example, it uses a parabolic reflector. What this means is that a light source is placed where the focus is. This causes the rays to bounce off the parabola line and ricochet parallel to the axis of symmetry. These particles of light being concentrated to emit an array of light beams represent the function of this parabolic example. However, regarding the real life application of this example, it is sometimes necessary to lower the amount of rays being parallel to the axis of symmetry. Therefore, a filament should be used to control the angle of the light rays. If the filament is placed behind the focus, then the light rays will converge. If placed in front of the focus, the ray will diverge instead. If placed above, then the ray will be directed downwards, with it being placed below causing the headlights to show light upwards.
        The vertex is behind the more important part in the headlights- behind the focus point. The directrix is not of huge importance as well since the main point of this example is to highlight the usage of the focus, axis of symmetry, and to an extent the vertex (because the vertex provides the curve which is needed to alter the direction of light reflected off of it). The axis of symmetry is of course in the middle of the parabola and like we said earlier, the more light rays that are reflected parallel to the axis of symmetry, the greater the concentration of light that will be emitted. For the value of p, the greater it is, the greater the distance the focus will be from the vertex, resulting in a wider headlight, which means the light rays covering more area. Overall, this real life application is a paramount example of how important the focus and axis of symmetry to particular aspects of life.

4.
In this video, the equation of a parabola is emphasized. Life I mentioned before, the vertical axis and horizontal axis dictate much of a parabola's information, as it influences the axis of symmetry, focus point and directrix. The equation (x-h)^2=4p(y-k) and (y-k)^2=4p(x-h) plays a huge part in this video as the lady goes on the explain the effects each one has on the shape of the graph as well as the focus point and directrix. An example is even shown as it portrays the steps to solving a parabola correctly.

4. References:

• http://www.wyzant.com/resources/lessons/math/algebra/conic_sections
• http://www.mathwarehouse.com/quadratic/parabola/focus-and-directrix-of-parabola.php
• https://people.richland.edu/james/lecture/m116/conics/conics.html
• http://www.pleacher.com/mp/mlessons/calculus/appparab.html
• http://xahlee.info/SpecialPlaneCurves_dir/Parabola_dir/parabola.html
• http://www.mathwarehouse.com/geometry/parabola/standard-and-vertex-form.php