2. Regarding the standard form of a parabola, if the parabola has a vertical axis of symmetry, then the equation is
(x-h)2=4p(y-k), with (h,k+p) being the ordered pair for the focus. A parabola with a horizontal axis of symmetry will have the standard equation of (y-k)^2=4p(x-h) and the focus ordered pair being (h+p,k). The difference between the two is whether x or y is in the front of the equation and where the p value goes in the ordered pair of the focus. Visually (graphically), a parabola looks like a curved line, with both arrows pointing in the same direction, but meeting in the middle along the aforementioned curved lines. What determines the direction of the parabola are two factors. If the value of p is positive, just like the graph, the parabola is bound to be going up or right.If p is negative, then of course, the parabola will go down or left.The second factor on determining the direction of the parabola is if the equation has an (x-h)^2 or (y-k)^2 as its standard form. If it is x^2, then the graph goes up or down. If its y^2. then its left or right. The size of the parabola depends on the value of |a|. The smaller the value of |a|,then the wider the graph. A parabola with a |a| of 0.3 will be much wider than one with an |a| of 1. This applies if the standard form is expressed as y=ax^2+bx+c. In this case we place a heavier emphasis on p.
An axis of symmetry shows the exact middle of a parabola where it touches the vertex. The vertex is the origin of the parabola, and its value depends on the h and k values of the standard form. Regarding its origin graphically, it is in between the focus and the directrix. The focus's value,as mentioned before, depends on if the graph's axis of symmetry is horizontal or vertical. If its vertical, then the ordered pair is (h,k+p).If its horizontal, (h+p.k) will be the ordered pair. The focus is situated WITHIN the parabola. What this means is that the focus will always be in the same direction as where the arrows of the parabolas point to. The directrix's value is the p value added or subtracted conversely to what it was added or subtracted for the focus. However, we do not write it as an ordered pair. We write it either equal to x or y, depending on if the value goes up or down, or in other words, on the the direction of the axis of symmetry. The value of p,as mentioned previously, takes the value of the coefficient of the non-squared coefficient of the variable and sets it to 4p. This value determines how far the focus and directrix will be from the vertex. A key note is that the directrix is always behind the parabola, or vertex, and the focus is always in front of the parabola,or vertex. The focus affects the shape of the parabola tremendously due to its connection with the eccentricity of the parabola. The closer the focus is to the parabola, the skinnier the parabola will be due to its relation with the difference between the focus and vertex being closer to 0. The closer a conic section is to 0, then the more circular it will be. Therefore, if the focus is farther away from the vertex, than the curves of the parabola will stretch and become less circular.
https://people.richland.edu/james/lecture/m116/conics/conics.html
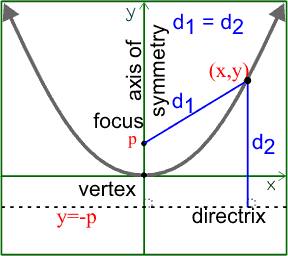
This picture depicts the various parts of the parabola. The vertex is now clearly shown as the origin of the parabola, since that is where all the other factors revolve around. The directrix is shown below the parabola, as the parabola protrudes upwards. The focus is between the two curves, and the axis of symmetry shows the middle of the parabola. The d1 and d2 lines showcase that the distance from the focus to a point on the parabola to the directrix is the same for both lines. Also, in this graph, we see that the focus is considerably farther away from the vertex than common examples with a p value such as 1/16, so the graph becomes wider.

http://xahlee.info/SpecialPlaneCurves_dir/Parabola_dir/parabola.html
3. A real life example of a parabola would be a car's headlights. In this example, to describe why it is a parabolic example, it uses a parabolic reflector. What this means is that a light source is placed where the focus is. This causes the rays to bounce off the parabola line and ricochet parallel to the axis of symmetry. These particles of light being concentrated to emit an array of light beams represent the function of this parabolic example. However, regarding the real life application of this example, it is sometimes necessary to lower the amount of rays being parallel to the axis of symmetry. Therefore, a filament should be used to control the angle of the light rays. If the filament is placed behind the focus, then the light rays will converge. If placed in front of the focus, the ray will diverge instead. If placed above, then the ray will be directed downwards, with it being placed below causing the headlights to show light upwards.
The vertex is behind the more important part in the headlights- behind the focus point. The directrix is not of huge importance as well since the main point of this example is to highlight the usage of the focus, axis of symmetry, and to an extent the vertex (because the vertex provides the curve which is needed to alter the direction of light reflected off of it). The axis of symmetry is of course in the middle of the parabola and like we said earlier, the more light rays that are reflected parallel to the axis of symmetry, the greater the concentration of light that will be emitted. For the value of p, the greater it is, the greater the distance the focus will be from the vertex, resulting in a wider headlight, which means the light rays covering more area. Overall, this real life application is a paramount example of how important the focus and axis of symmetry to particular aspects of life.
4.
In this video, the equation of a parabola is emphasized. Life I mentioned before, the vertical axis and horizontal axis dictate much of a parabola's information, as it influences the axis of symmetry, focus point and directrix. The equation (x-h)^2=4p(y-k) and (y-k)^2=4p(x-h) plays a huge part in this video as the lady goes on the explain the effects each one has on the shape of the graph as well as the focus point and directrix. An example is even shown as it portrays the steps to solving a parabola correctly.
4. References:
- http://www.wyzant.com/resources/lessons/math/algebra/conic_sections
- http://www.mathwarehouse.com/quadratic/parabola/focus-and-directrix-of-parabola.php
- https://people.richland.edu/james/lecture/m116/conics/conics.html
- http://www.pleacher.com/mp/mlessons/calculus/appparab.html
- http://xahlee.info/SpecialPlaneCurves_dir/Parabola_dir/parabola.html
- http://www.mathwarehouse.com/geometry/parabola/standard-and-vertex-form.php
No comments:
Post a Comment